BASIC MATHEMATICS OF "ANGRY BIRDS"
"Angry Birds" has been a popular touchscreen game that quenched the
boredom and leisure of many since its inception in 2010. The
mathematics behind the "Angry Birds" is found in describing the
path that the bird takes to get to its target.
Figure 1 provides a schematic diagram of the
game. The goal is to launch the bird, by drawing the slingshot, to
target green pigs situated on the other side of the screen. There is
a story line behind the animosity the birds have over the pigs, but
it suffices to say that they are motivated enough to sacrifice
themselves as avian cannonballs.
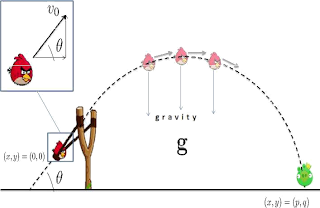 |
| Figure 1: Schematic diagram of the "Angry Birds" game. The inset is a zoomed-in version of the bird on the slingshot. |
With a bird riding on it, the slingshot is drawn
tight such that it makes a certain angle \(\theta\) with respect to the horizontal within the reasonable interval
\( \left[0,\frac{\pi}{2}\right] \). This is referred to as the launching angle. It is
also the angle between the horizontal and an arrow
that represents the take-off velocity of the bird (see
zoomed-in inset of Fig. 1). When the slingshot is released, the bird takes off with initial speed \(v_0\) in the
direction denoted by the arrow.
Since the game is laid in 2d (i.e., on a plane), then position can be described by coordinates \( (x,y) \), where \(x\) denotes position along the horizontal axis and \(y\) position along the vertical axis. Let us take the origin of the axis as the launching point for the angry bird, i.e., \( (0,0) \) as depicted in Fig. 1. The position of the target (e.g., the green pig) is at \( (p,q) \). For the sake of simplicity, let us take \( q \approx 0 \) (i.e., the target is situated at a vertical level close to the level from which the bird is launched).
During its flight, the bird changes its position \( (x,y) \) so that \( x = x(t) \) and \( y = y(t) \) are functions of time \(t\). This motion, known as projectile motion, is a combination of both the forward horizontal motion and falling vertical motion. Indeed, not all falling objects fall straight down to the ground. It all depends on how the object is launched. Thanks to Galileo Galilei and Isaac Newton, who laid the foundations of our current understanding about objects in motion in the 17th century, we can write down the mathematical equations to quantify motion.
The displacement is generally a product of the speed of motion and time. According to the findings of Galileo, the bird's horizontal speed should not change throughout its flight since nothing is pushing the bird to move forward horizontally (Note: the game always takes place on a windless day so that one can conveniently neglect the effect of air). That means \( x(t) = (v_0 \cos \theta) t \) where \(v_0 \cos \theta \) is the component of the bird's initial motion along the horizontal axis. On the other hand, some invisible agent is pulling the bird down so that it is bound to fall back to the ground. According to Newton, this agent is known as gravity which makes falling objects close enough to the ground (i.e., anything lower than Mt. Everest) gain speed at a constant rate, \(g\), on its way down. Consequently, \( y(t) = (v_0 \sin \theta) t - g\left(\frac{t^2}{2}\right) \), where \( v_0 \sin \theta \) is the component along the vertical axis of the bird's initial motion. In summary, the equations of motion in terms of time t are: \[ \begin{align} x(t) &= (v_0 \cos \theta) t \\ y(t) &= (v_0 \sin \theta) t - g\left(\frac{t^2}{2}\right) \end{align} \]
Since the game is laid in 2d (i.e., on a plane), then position can be described by coordinates \( (x,y) \), where \(x\) denotes position along the horizontal axis and \(y\) position along the vertical axis. Let us take the origin of the axis as the launching point for the angry bird, i.e., \( (0,0) \) as depicted in Fig. 1. The position of the target (e.g., the green pig) is at \( (p,q) \). For the sake of simplicity, let us take \( q \approx 0 \) (i.e., the target is situated at a vertical level close to the level from which the bird is launched).
During its flight, the bird changes its position \( (x,y) \) so that \( x = x(t) \) and \( y = y(t) \) are functions of time \(t\). This motion, known as projectile motion, is a combination of both the forward horizontal motion and falling vertical motion. Indeed, not all falling objects fall straight down to the ground. It all depends on how the object is launched. Thanks to Galileo Galilei and Isaac Newton, who laid the foundations of our current understanding about objects in motion in the 17th century, we can write down the mathematical equations to quantify motion.
The displacement is generally a product of the speed of motion and time. According to the findings of Galileo, the bird's horizontal speed should not change throughout its flight since nothing is pushing the bird to move forward horizontally (Note: the game always takes place on a windless day so that one can conveniently neglect the effect of air). That means \( x(t) = (v_0 \cos \theta) t \) where \(v_0 \cos \theta \) is the component of the bird's initial motion along the horizontal axis. On the other hand, some invisible agent is pulling the bird down so that it is bound to fall back to the ground. According to Newton, this agent is known as gravity which makes falling objects close enough to the ground (i.e., anything lower than Mt. Everest) gain speed at a constant rate, \(g\), on its way down. Consequently, \( y(t) = (v_0 \sin \theta) t - g\left(\frac{t^2}{2}\right) \), where \( v_0 \sin \theta \) is the component along the vertical axis of the bird's initial motion. In summary, the equations of motion in terms of time t are: \[ \begin{align} x(t) &= (v_0 \cos \theta) t \\ y(t) &= (v_0 \sin \theta) t - g\left(\frac{t^2}{2}\right) \end{align} \]
By eliminating \(t\), an equation for \( y = y(x) \) can be written as follows, \[ y(x) = (\tan \theta)x - \left(g\frac{{v_0}^2}{2}{\cos}^2 \theta\right)x^2 \] which is an equation for a parabola (concave downward) on the Cartesian plane. Indeed if you observe the paths traced out in the game, they do resemble the parabola.
What is more interesting is that one could maximize the range (i.e.,how far the bird projectile would land away from the slingshot for any given initial speed \(v_0\)) by simply adjusting the launching angle. In order to determine the optimal angle \(\theta^{\ast}\), one solves for \(t\) for \( y = q \approx 0 \). This leads to a quadratic equation whose roots are: \[ t^{\ast} = 0 \text{ and } t^{\ast} = \frac{1}{g}(2 v_0 sin \theta) \]
What is more interesting is that one could maximize the range (i.e.,how far the bird projectile would land away from the slingshot for any given initial speed \(v_0\)) by simply adjusting the launching angle. In order to determine the optimal angle \(\theta^{\ast}\), one solves for \(t\) for \( y = q \approx 0 \). This leads to a quadratic equation whose roots are: \[ t^{\ast} = 0 \text{ and } t^{\ast} = \frac{1}{g}(2 v_0 sin \theta) \]
The only relevant solution is the latter one, which is now used to determine the final position \( x(t^{\ast}) \). The range \(R\) is simply the difference between the horizontal position of the angry bird, i.e., \( x(0) = 0 \) and the final position; hence, \[ R= (v_0 \cos \theta)t^{\ast} = (v_0 \cos \theta)\left(\frac{1}{g}\right)(2v_0 \sin \theta) = \left(\frac{1}{g}\right)({v_0}^2 \sin 2\theta) = R(\theta). \]
By using the basic concepts of differential calculus, \(R(\theta)\) is maximized such that \(\frac{dR}{d\theta} = 0 \) and \(\frac{d^2R}{d^2\theta} < 0\). Hence, \[ \begin{eqnarray*}
\left.\frac{dR}{d\theta}\right|_{\theta=\theta^*} &= &
\left.\frac{v_0^2}{g}\left(2\cos2\theta\right)\right|_{\theta=\theta^*}
=0\\
& &\Rightarrow \cos2\theta^* = 0 \Rightarrow 2\theta^* =
\frac{\pi}{2} \Rightarrow \theta^* = \frac{\pi}{4} \equiv
45^{\circ}\, .
\end{eqnarray*}
\]
Consequently, \(\frac{d^2R}{d^2\theta} = -\sin 2\theta < 0 \) for \( \theta = \theta^{\ast} \). Therefore, \( \theta^{\ast} = 45^{\circ}\) does give the maximum range. This can be verified through the game. One would see that if \(\theta > 45^{\circ}\), the angry bird can go up so high but does not really travel forward by as much. On the other hand, if \(\theta\) is too small, the bird lands on the ground right away before being able to move appreciably forward.
Consequently, \(\frac{d^2R}{d^2\theta} = -\sin 2\theta < 0 \) for \( \theta = \theta^{\ast} \). Therefore, \( \theta^{\ast} = 45^{\circ}\) does give the maximum range. This can be verified through the game. One would see that if \(\theta > 45^{\circ}\), the angry bird can go up so high but does not really travel forward by as much. On the other hand, if \(\theta\) is too small, the bird lands on the ground right away before being able to move appreciably forward.
So next time you play "Angry Birds", find a protractor and mark your screens with the special angle \(45^{\circ} = \frac{\pi}{4}\). It might be quite useful in aiming for those nasty swines.
ABOUT THE AUTHOR:
Dranreb Earl Juanico is an Assistant Professor at the Ateneo de Manila University. He obtained his B.S., M.S., and Ph.D. in Physics at the University of the Philippines in 2002, 2004 and 2007, respectively.
Dranreb Earl Juanico is an Assistant Professor at the Ateneo de Manila University. He obtained his B.S., M.S., and Ph.D. in Physics at the University of the Philippines in 2002, 2004 and 2007, respectively.
OLYMPIAD CORNER
from the 14th Turkish Mathematical Olympiad, 2006
Problem: Points
\(E\) and \(F\) on side \(CD\) of a convex quadrilateral \(ABCD\) are
given such that \(DE = FC\). The circumcircles of triangles \(ADE\) and
\(ACF\) meet again at \(K\) and those of \(BDE\) and \(BCF\) meet again
at \(L\). Show that the points \(A, B, K, L\) lie on a circle.
Solution:
Let
\(M\) be intersection of \(DC\) and \(AK\), and \(N\) be
theintersection of \(DC\) and \(BL\). Based on the powers of the point
\(M\) with respect to the circles \(ADE\) and \(AFC\), we have \[ ME\cdot MD=MK\cdot MA=MF\cdot MC \hspace{20px} (1) \]
Solution:
Using the derived equality \(ME\cdot MD=MF\cdot MC\) and the given \(DE=FC\),\[ \begin{align*} ME\cdot MD &= MF\cdot MC \\ ME\cdot ( ME+DE) &= MF\cdot ( MF+FC) \\ (ME)^2+ME\cdot DE &= ( MF)^2+MF\cdot FC \\ (ME)^2+ME\cdot DE &= (MF)^2+MF\cdot DE \\ (ME)^2-(MF)^2+ME\cdot DE-MF\cdot DE &= 0 \\ (ME-MF)(ME+MF)+DE(ME-MF) &= 0 \\ (ME-MF) (ME+MF+DE) &= 0 \end{align*} \]
Noting that \(ME+MF+DE>0\), then \(ME=MF\) and
hence \(M\) is the midpoint of segment \(FE\). Since \(DE=FC\), then
\(MD=MC\) and therefore \(M\) is the midpoint of segment \(CD\).
Likewise, based on the powers of point \(N\), we have \[ NE\cdot ND=NL\cdot NB=NF\cdot NC \hspace{20px} (2) \] where can it also be shown, using the same arguments as above, that \(N\) is the midpoint of segment \(CD\). Hence \(M\) and \(N\) represent the same point.
From \((1)\) and \((2)\), we have \[ MK\cdot MA\underset{(1)}{=}ME\cdot MD\underset{M=N}{=}NE\cdot ND\underset{(2)}{=}NL\cdot NB\underset{M=N}{=}ML\cdot MB \] which tells us that \(A,B,K,L\) all lie on a circle.
Likewise, based on the powers of point \(N\), we have \[ NE\cdot ND=NL\cdot NB=NF\cdot NC \hspace{20px} (2) \] where can it also be shown, using the same arguments as above, that \(N\) is the midpoint of segment \(CD\). Hence \(M\) and \(N\) represent the same point.
From \((1)\) and \((2)\), we have \[ MK\cdot MA\underset{(1)}{=}ME\cdot MD\underset{M=N}{=}NE\cdot ND\underset{(2)}{=}NL\cdot NB\underset{M=N}{=}ML\cdot MB \] which tells us that \(A,B,K,L\) all lie on a circle.
PROBLEMS
- Evaluate \[1+\frac{1}{2}+\frac{2}{2}+\frac{1}{2}+\frac{1}{3}+\frac{2}{3}+\frac{3}{3}+\frac{2}{3}+\frac{1}{3} +\ldots+\frac{1}{n}+\frac{2}{n}+\ldots+\frac{n}{n}+\frac{n-1}{n}+\ldots+\frac{1}{n}.\]
- \(ABCD\) is a square, \(E\) and \(F\) are the midpoints of the sides \(AB\) and \(BC\) respectively. If \(M\) is the point of intersection of \(CE\) and \(DF\), prove that \(AM\) = \(AD\).
- If \(A, B\) and \(C\) are the measurements of the angles in each of the vertices of the triangle \(ABC\), show that \[ \cos A + \cos B + \cos C \leq \frac{3}{2}. \]
We welcome readers to submit solutions to the problems posed below for
publication consideration. Solutions must be preceded by the solver's
name, school affiliation and year level. The deadline for submission is
December 3, 2011 (extended to December 10, 2011).

No comments:
Post a Comment