Origami and Paper Folding
Origami is the traditional Japanese art of paper folding. It involves transforming a piece of paper using only folds and creases. There are no cutting and gluing in strict origami. It is amazing how different geometric shapes and three-dimensional figures can be made just by folding papers. One can discover lines, polygons and lines inside an origami model.
But did you know that, aside from geometry, algebra is also present in paper folding? Without the goal of forming a three-dimensional model, simple paper folding can help one solve various equations.
Let us look at how paper folding can be used to form various geometric concepts. We will also construct two origami models and discover the beautiful pattern inside our models. Finally, we show how simple paper folding is used to solve a cubic equation (a polynomial of degree 3).
Basic Geometric Shapes Using Origami
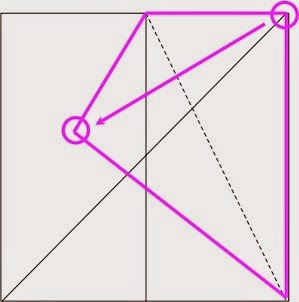
Geometric concepts are clearly present in origami and simple paper folding. Everyone knows how to fold a piece of paper in half or even in quarters just by simply folding a folded paper in half. For that matter, one can fold in any powers of 2: \(\dfrac{1}{8}\), \(\dfrac{1}{16}\), etc. But do you know how to fold a paper in exactly 3 parts? Moreover, you may easily divide an angle into 2 equal parts by simple paper folding, but can you trisect an angle (divide the angle into 3 equal parts)?
(Folding a paper in thirds using a square)
7.

(Folding a paper in thirds using a rectangle)
7.

(Trisecting an angle)
More Origami
It is fun to construct different figures by paper folding. We will do simple origami. What's so special about them? When we unfold the figure, we will reveal beautiful patterns (unintentionally?) arising from our paper folding.
(Yacht)
1.  |
2.  |
3.  |
4.  |
5.  |
6.
|  |
| (Reverse Fold) |
|
7.  |
8.  |
9.

(Bird)
Solving Real Roots Using Paper Folding
Consider \[ x^3 + b x^2 + c x + d = 0 \]where \(b\), \(c\), \(d \in \mathbb{R}\). This is a polynomial of degree 3 (also called a cubic polynomial).
To get the real roots using paper folding:
- Let \(P\) denote \((0, 1)\), and \(Q\) denote \((-b + d, c)\).
- Make a single fold that simultaneously places \(P\) on a point \(P'\) on \(y = -1\) and places \(Q\) on a point \(Q'\) on \(x = -b - d\). This can be done in different ways, especially if the cubic polynomial has 3 real roots (in that case, 3 possible folds can be done).
- The \(x\)-intercept of the fold line is a root of \(x^3 + b x^2 + c x + d = 0\).
As an example, consider the equation \[ x^3 - 2x^2 - x + 2 = 0. \]Thus, \(b = -2\), \(c = -1\) and \(d = 2\).
- The points are \(P(0,1)\) and \(Q(-(-2) + 2, -1) = Q(4, -1)\).
- Place \(P\) on a point \(P'\) on \(y = -1\) and \(Q\) on a point \(Q'\) on \(x = -(-2) - 2 = 0\).
- The possible folds are as follows:
Conclusion
Origami and paper folding are fun to do. There are numerous complicated figures that one can make using this traditional Japanese paper art. But as we have seen, there is more to folding paper than meets the eye. Perfect geometric figures may be formed and discovered when paper are folded accordingly. Moreover, who knew that paper folding can be utilized to solve a cubic equation? These things surely put the fun in math!
ABOUT THE AUTHOR:
Patrick Vincent N. Lubenia is an Instructor at the Ateneo de Manila University. He obtained his B.S in Mathematics and M.S. in Applied Mathematics at the University of the Philippines Diliman in 2008 and 2012, respectively. He is currently finishing his M.S. in Finance in the same university.
OLYMPIAD CORNER
from the International Mathematical Olympiad Shortlist, 2010
Problem: Find the least positive integer \(n\) for which there exists a set \(\{s_{1},s_{2},\ldots,s_{n}\}\) consisting of \(n\) distinct positive integers such that \[ \left( 1-\frac{1}{s_{1}}\right) \left( 1-\frac{1}{s_{2}}\right) \cdots \left( 1-\frac{1}{s_{n}}\right) = \frac{42}{2010}. \]
Solution:
Suppose that the desired numbers exist for some \(n\). We may assume without loss of generality that \[ s_{1}<s_{2}<\cdots <s_{n}. \]Note that \(s_{1}\) should be an integer greater than 1, otherwise \(1-\frac{1}{s_{1}}=0\). This implies that \[ 2\leq s_{1}\leq s_{2}-1\leq \cdots \leq s_{n}-\left( n-1\right) \]therefore \[ \begin{eqnarray*} s_i &\geq &i+ 1 \\ \frac{1}{s_i} &\leq &\frac{1}{i+1} \\ 1 - \frac{1}{s_i} &\geq &1-\frac{1}{i+1} \end{eqnarray*} \]for each \(i = 1, 2, \ldots, n\).
Moreover, since the denominator of \(\frac{42}{2010}=\frac{7}{5\cdot 67}\) is divisible by 67, some of the \(s_{i}^{\prime }\)'s should be divisible by 67, and hence \[ \begin{eqnarray*} s_n &\geq &s_i \geq 67 \\ 1-\frac{1}{s_n} &\geq &1-\frac{1}{67} = \frac{66}{67}. \end{eqnarray*} \]This means that\[ \begin{eqnarray*}\frac{42}{2010} &=&\left(1-\frac{1}{s_1}\right) \left(1-\frac{1}{s_2}\right) \cdots \left(1-\frac{1}{s_{n-1}}\right)\left(1-\frac{1}{s_n}\right) \\ &\geq &\left(1-\frac{1}{2}\right) \left(1-\frac{1}{3}\right) \cdots \left(1-\frac{1}{n}\right) \left(\frac{66}{67}\right) \\ &=&\left(\frac{1}{2}\right) \left(\frac{2}{3}\right) \cdots \left(\frac{n-1}{n}\right) \left(\frac{66}{67}\right) \\ &=&\frac{66}{67n} \end{eqnarray*} \]therefore\[ n\geq \frac{\left( 2010\right) (66)}{\left( 42\right) \left( 67\right) }= \frac{330}{7}>47 \]and hence \(n\geq 48\).
Now we are left to show that there exists a set \(s_1, s_2, \ldots, s_{48} \) that satisfies the equality. Consider the set \[ \{2,3,\ldots,32,33,36,37,\ldots,50,67\} \]which contains exactly 48 numbers. Then \[ \begin{eqnarray*} &&\left(1-\frac{1}{2}\right) \cdots \left(1-\frac{1}{33}\right) \left(1 - \frac{1}{36}\right) \cdots \left(1-\frac{1}{50}\right) \left(1-\frac{1}{67}\right) \\ &=&\left[ \left(\frac{1}{2}\right) \cdots \left(\frac{32}{33}\right) \right] \left[ \left(\frac{35}{36}\right) \cdots \left(\frac{49}{50}\right)\right] \left(\frac{66}{67}\right) \\ &=&\left(\frac{1}{33}\right) \left(\frac{35}{50}\right) \left(\frac{66}{67}\right) \\ &=&\frac{7}{335} = \frac{42}{2010}. \end{eqnarray*} \]The least positive integer \(n\) is therefore equal to 48.
PROBLEMS
- Show that if \(2^{n}-1\) is prime, then \(n\) must be prime.
- Given a positive integer \(n\), let \(p\left(n\right)\) be the product of the nonzero digits of \(n\). Determine the value of \( p\left(1\right) + p\left(2\right) + \cdots + p\left(999\right) + p\left(1000\right). \)
- In \(\triangle ABC\), \(D\), \(E\) are on \(BC\) and \(CA\) respectively, and \(BD:DC=3:2\), \(AE:EC=3:4\). \(AD\) and \(BE\) intersect at \(M\). Given that the area of \(\triangle ABC\) is \(1\), find the area of \(\triangle BMD\).
We welcome readers to submit solutions to the problems posed below for publication consideration. Solutions may ONLY be submitted online via vantonio@ateneo.edu. Solutions must be preceded by the solver's name, school affiliation and year level. The deadline for submission is 12:30 PM November 29, 2014.
SOLUTIONS
(for November 8, 2014)
Let \(a\), \(b\), \(c\) be positive integers with the properties: \(a^{3}\) is divisible by \(b\), \(b^{3}\) is divisible by \(c\), \(c^{3}\) is divisible by \(a\). Show that \(\left(a+b+c\right)^{13}\) is divisible by \(abc\). (Taken from Polish and Austrian Mathematical Olympiads 1981-1995 by M. Kuczma and E. Windischbacher)
(solved by Farrell Eldrian Wu [MGC New Life Academy])
SOLUTION:
Note that each of the terms in the expansion of \(\left(a+b+c\right)^{13}\) has the form \(a^{l}b^{m}c^{n}\), where \(l\), \(m\), and \(n\) are nonnegative and \(l+m+n=13\). Our goal is to show that each of the terms is divisible by \(abc\).
If \(l,m,n\geq1\), then this is trivial. Let us consider the case when one of \(l,m,n=0\).
Suppose \(l=0\). This means we have \(b^{m}c^{n}\), where \(m+n=13\).
CASE 1:
If \(m=13\), \(n=0\), then we have \(b^{13}=b\cdot b^{3}\cdot b^{9}=b\left(cp\right)\left(c^{3}p^{3}\right)\) for some integer \(p\), since \(b^{3}\) is divisible by \(c\). Moreover, \[ b^{13} = b\left(cp\right)\left(c^3p^3\right) = b\left(cp\right)\left(aqp^3\right) \]for some \(q\), since \(c^{3}\) is divisible by \(a\). This means that the product \(a^{0}b^{13}c^{0}\) is divisible by \(abc\).
CASE 2:
If \(10\leq m\leq12\), \(1\leq n\leq3\), then we have \(b^{m}c^{n}=b\cdot c\cdot b^{9} \left(b^{m-10}c^{n-1}\right)\), which is divisible by by \(abc\) (since, based from the previous case, \(b^{9}\) is divisible by \(a\)).
CASE 3:
If \(1\leq m\leq9\), \(4\leq n\leq12\), then we have \(b^{m}c^{n}=b\cdot c\cdot c^{3}\left(b^{m-1}c^{n-4}\right)\), which is divisible by \(abc\) (since \(c^{3}\) is divisible by \(a\)).
\textit{CASE 4:}
If \(m=0\), \(n=13\), then we have \(c^{13}=c\cdot c^{3}\cdot c^{9}=c\left(ar\right)\left(a^{3}r^{3}\right)\), for some integer \(r\). Since \(a^{3}\) is divisible by \(b\), we can see that \(c^{13}\) is divisible by \(abc\).
In all cases, we see that \(b^{m}c^{n}\) is divisible by \(abc\). We can proceed with a similar proof for when \(m=0\), and for \(n=0\). This means that \(\left(a+b+c\right)^{13}\) is divisible by \(abc\).
An exam with \(k\) questions is presented to \(n\) students. A student fails the exam if he gets less than half the answers right. We say that a question is easy if more than half of the students get it right. Decide if it is possible that
- All students fail even though all the questions were easy.
- No student fails even though no question was easy.
(Estonia 2007)
(solved by Farrell Eldrian Wu [MGC New Life Academy])
SOLUTION:
- For the first case, if all questions were easy, then more than \(\dfrac{n}{2}\) students are able to to get each of the \(k\) questions right. So \(T>k\cdot\dfrac{n}{2}\) (note that this is a strict inequality).
On the other hand, if each of the \(n\) students failed, then all of them got less then \(\dfrac{k}{2}\) questions right. This means that \(T<n\dfrac{k}{2}\) (again, a strict inequality). Combining the two conditions makes the first case impossible.
- For the second case, if no question was easy, then at most \(\left\lceil \dfrac{n}{2}\right\rceil \) students got each of the \(k\) questions right. So \(T\leq k\left\lceil \dfrac{n}{2}\right\rceil \).
Now, if no student fails, then each of the \(n\) students got at least \(\left\lceil \dfrac{k}{2} \right\rceil\) questions right. Then \(T\geq n\left\lceil \dfrac{k}{2}\right\rceil\). Combining the two conditions, we have \(n \left\lceil \dfrac{k}{2} \right\rceil \leq T \leq k \left\lceil \dfrac{n}{2} \right\rceil \), which means \(T = \dfrac{nk}{2}\), where \(n\) and \(k\) are both even.
Specifically, if a labeling will be implemented on the students \(\left(1,2,\dots,n\right)\) and questions \(\left(1,2,\ldots,k\right)\), then student \(m\) should answer \(l\) questions, where \(m\) and \(l\) have the same parity.
\(2014\) points are given on a circle. They are split into \(1007\) pairs and each pair is joined by a segment. Find the probability that no two of these segments intersect. (Taken from Problem-Solving Methods in Combinatorics by Pablo Soberon)
(solved by Farrell Eldrian Wu [MGC New Life Academy])
SOLUTION:
First, we count the number of ways to split the \(2n\) points without considering the intersections. We choose \(n\) points first, then choose which of the remaining \(n\) points will be paired up with the initial group. Note that in choosing the pairs, the order matters. So this can be done in \({\displaystyle \binom{2n}{n}n!}\) ways. However, we still need to consider that in each segment, the order in which the vertices were chosen does not matter. So, upon incorporating the double count for each segment, we have \[ \dfrac{{\displaystyle \binom{2n}{n}n!}}{2^{n}} \]ways of pairing the \(2n\) points.
Now, we introduce a sequence of numbers \(a_n\), where \(a_n\) is defined to be the number of ways to connect \(2n\) points on a circle where the connecting segments will not intersect. For the purpose of completeness, we define \(a_0=1\). In addition, we label the points on the circle with \(1,2,\ldots,2n\).
We connect \(1\) with any vertex \(k\). The segment will divide the circle into two sections. Note that the remaining \(2n-2\) vertices should still be paired up, and if \(k\) is odd, then there will be one section (the one between \(1\) and \(k\)) with an odd number of points, which means that one point in that section will have to be connected to one point on the other section, and the segment formed will intersect with the initial segment. This means that \(k\) must be even.
So \(1\) must be connected to \(2p\). Then the remaining \(2p-2\) points between \(1\) and \(2p\) must be paired up between themselves (same is true for the other section, which contains the points \(2p+1\) to \(2n\), a total of \(2n-2p\) points). By our definition, there are \(a_{p-1}a_{n-p}\) ways that this can be done. So, upon doing this for all \(p\), we get \[ \begin{align*} a_{0} & = 1\\ a_{n} & = a_{n-1}a_{0}+a_{n-2}a_{1}+\cdots+a_{0}a_{n-1}, \end{align*} \]which follows the definition of Catalan numbers. The closed form of numbers in this sequence is given by \[ a_{n}=\frac{{\displaystyle \binom{2n}{n}}}{n+1}. \]Thus, the probability of pairing the \(2n\) points and forming non-intersecting segments is given by \[ \dfrac{\frac{{\displaystyle \binom{2n}{n}}}{n+1}}{\dfrac{{\displaystyle \binom{2n}{n}n!}}{2^{n}}}=\frac{2^{n}}{\left(n+1\right)!}. \]In our case, we just have \(n=1007\), so the probability is \(\dfrac{2^{1007}}{1008!}\).